DC metrology
Question 1:
Define the following metrological terms:
- �
- Uncertainty
- �
- Accuracy
- �
- Error
- �
- Precision
- �
- Traceability
Notes:
The words äccuracy" and "precision" are often (incorrectly) interchanged with one another. They have distinct and separate meanings, though.
Regarding the word "traceability," you might want to elaborate on electrical metrology as a career in itself. Maintaining international measurement standards is a work-intensive endeavor, and qualified electronics people at all levels of expertise (technicians, engineers, researchers, scientists) are needed in many locations around the world to maintain the system. Though it may sound boring, metrology is essential to state-of-the art scientific research as well as modern industry.
Question 2:
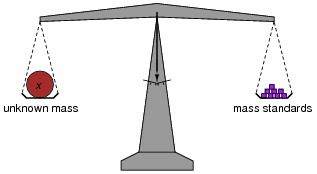
In chemistry laboratories, balance scales are used to precisely measure the mass of various substances. How, exactly, is a laboratory "balance" scale used? What component of the scale primarily determines its accuracy?
|
|
Notes:
The important point I wish to communicate with this question is that the scale does nothing but indicate a condition of balance (zero excess mass on either side). As such, the primary source of accuracy in this measurement system does not lie within the scale mechanism itself! This is an important quality of a measurement system: to isolate sources of inaccuracy to very specific portions of the system, where they may be tightly controlled.
Question 3:
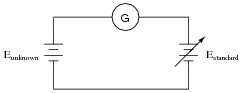
Explain how this electrical system functions in a similar manner to a laboratory "balance" scale:
|
|
The circle with the letter "G" in it is a symbol for a galvanometer. What practical purpose might a system like this serve?
Notes:
The first question your students are likely to ask is, "What is a galvanometer?" Let them do the research on this question! The answer is easy to find.
Next, your students will have to explain how this system may be used to do something practical. Just as a laboratory balance-beam serves the purpose of measuring mass, this system also measures something. Challenge your students to draw analogies between the components of this system and the components of a laboratory balance. What essential feature must the Estandard voltage source have in order for this to be a useful measurement system?
Question 4:
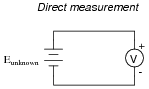
If a voltmeter is to be used to directly measure the voltage of an unknown source, it must first be calibrated so as to ensure an accurate measurement:
|
|
What is the minimum number of points along the meter's range that it needs to be calibrated at, given the assumption of perfectly linear response?
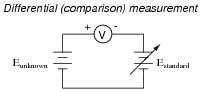
If a voltmeter is to be used to measure the voltage of an unknown source, as a differential indicator only, what is the minimum number of points along its range that it needs to be calibrated at?
|
|
A voltmeter used for differential measurement need only be calibrated at a single point along its range, and that single point is zero.
Notes:
Ask your students if the two calibration points on the meter's range should be close together, or far apart, for the best (most comprehensive) calibration possible.
Discuss the easier calibration requirements of the differential meter. Challenge your students with this question: "Does the measurement linearity of a voltmeter matter as much if it is used to make a differential measurement, as compared to if it is used to make a direct measurement?" Why or why not?
Question 5:
Explain the simplest way to perform a single-point calibration on a highly sensitive, precision voltmeter. How do you ensure the voltmeter is receiving a fixed input of known quantity, especially without having expensive calibration equipment available?
Notes:
Challenge your students with this question: Ïf zero is an appropriate signal to use for a single-point calibration, then why not just leave the two test leads disconnected? Why should you short them together?"
If you happen to have a sensitive voltmeter available in the classroom, the answer may be demonstrated with ease. This is especially true if you place the voltmeter in the ÄC millivolt" range so it picks up stray power-line voltages from nearby electrical devices and utilities.
Question 6:
This voltage divider should output half the battery's voltage between points A and B:
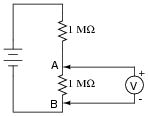
|
|
However, if you perform this same experiment using a real voltmeter, the measurement obtained with the meter will be substantially different from what should be there, based on a prediction of 1/2Ebattery. Explain why the voltmeter registers as it does. What is it about this circuit that causes the measurement to be so far off from the prediction, when we know full well that other voltage divider circuits we've constructed do not exhibit any significant error?
Notes:
Meter "loading" is a serious problem in electrical metrology. It is a basic principle of measurement that a measuring instrument always impacts the quantity being measured, to some extent. In cases like this, the extent of impact is severe.
For those instructors with some background in quantum physics, please refrain from perpetuating the myth that meter loading is an example of Heisenberg's Uncertainty Principle. The Uncertainty Principle has nothing to do with the impact of a measuring instrument on something we measure. Rather it describes an uncertainty inherent to the quantity itself. If you want to share a true electrical example of this uncertainty principle with your students, wait until they study harmonics and spectrum analyzers, where you can tell them it is impossible to measure both the instantaneous amplitude of a signal and the frequency of a signal with unlimited certainty.
Question 7:
The following voltmeter circuit avoids problems of "loading" when measuring high-resistance voltage sources. Describe how to operate this circuit, and how loading error is eliminated by using such a potentiometric instrument:

|
|
Notes:
"Potentiometric" DC voltage measurements used to be commonplace in industry prior to the advent of precision electronic voltmeters with high-resistance inputs. The technique, though, is certainly not obsolete, and in fact is still employed in metrological laboratories worldwide to obtain the most accurate (no-load) voltage measurements possible.
It is impressive to have students build a potentiometric voltmeter circuit using a cheap analog VOM (Volt-Ohm-Milliammeter), and have it outperform a direct-reading, laboratory-quality digital voltmeter costing hundreds of dollars! The greater the resistance inherent to the voltage source being measured, the more severe the loading error of any voltmeter, and the more a potentiometric instrument proves its worth.
Question 8:
General metrology used to be based upon standard artifacts, but the modern scientific trend is toward intrinsic standards. Explain what these two terms mean, as well as their significance in scientific work.
Notes:
A great example of an ärtifact" standard is the metal bar which used to be the international standard for the "meter" (metric unit of length). Ask your students how convenient it would be for scientists working around the world to calibrate their equipment if the only primary standard for length measurement were a single bar of metal. What benefits may be derived from the use of ïntrinsic" standards?
An excellent example of an easily-accessed intrinsic standard is the standard for time, available via shortwave radio: 5 kHz, 10kHz, 15 kHz, and 20 kHz (there are other frequencies, too). Have any of your students heard of timepieces that synchronize themselves to an ätomic clock"? With a shortwave radio, they can tune into that same atomic clock's broadcast and synchronize their own wristwatches! This is an excellent discussion activity, and a great way to garner student interest in what is potentially a dull subject.
Ask your students whether or not the existence of intrinsic standards negates the purpose of artifacts. That is, does anyone use artifacts anymore? Why or why not?
Question 9:
What technology is currently regarded as state-of-the-art for reproducing the standard volt?
Notes:
Questions like this will never become obsolete, even though the answer may. At the time of this writing (August 2003), the internationally recognized technology for the standard volt is based on a quantum phenomenon known as the Josephson Junction effect.
Question 10:
What technology is currently regarded as state-of-the-art for reproducing the standard ohm?
Notes:
Questions like this will never become obsolete, even though the answer may. At the time of this writing (August 2003), the internationally recognized technology for the standard volt is based on a quantum phenomenon known as the Quantum Hall Effect.
Question 11:
Calibration laboratories often make reference to Test Uncertainty Ratios (TUR's), normally holding to a ratio of 4:1 or more when performing calibration work on instruments. What does this figure mean?
Notes:
While your students may never have to calculate TUR's, it is still important for them to know what the general principle is. If any of them experience difficulty understanding the concept, ask them if it makes any sense to use a ruler to check the calibration of a micrometer, or to use a wristwatch to check the long-term stability of a laboratory-grade chronograph.
